Vol49　三角形の面積

次の三角形の面積を求めてください。∠B＝30°、AB＝9、BC＝12です。

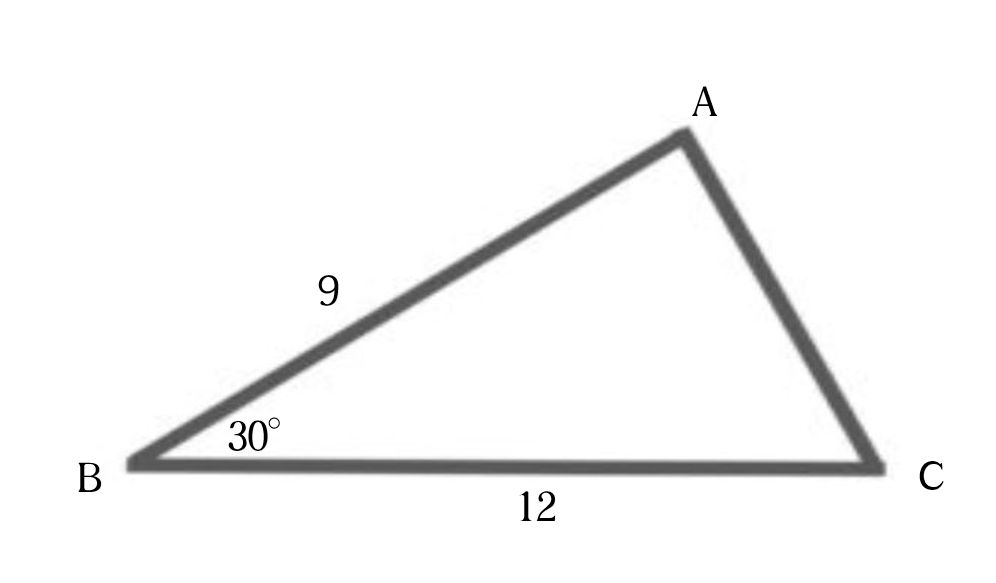
三角定規の三角形を頭に浮かべてください。30°、60°、90°の組み合わせ、45°2つと90°の直角二等辺三角形の組み合わせがあります。三角形の難しい問題はこれが基礎になっている事が多く、30°、45°、60°を見たら三角定規を思い出しましょう。どうやって解いたら良いのか判らない三角形の面積を求める問題の場合、30°、45°、60°の角度がどこかにあると、うまく補助線を引いて、二つの三角定規の形にならないか考えてみましょう。

解答　まずは下の図のように、AからBCに垂線を降ろして、BCとの交点をHとします。

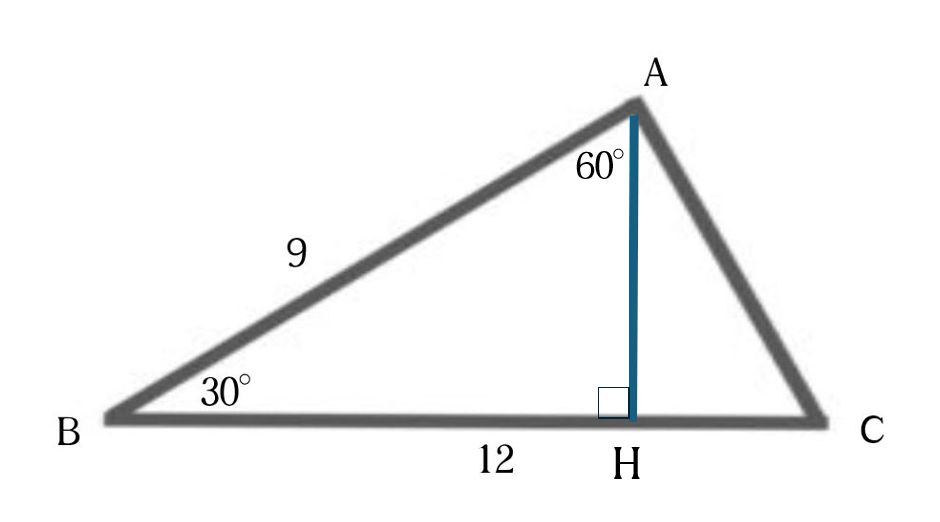
三角形ABHは三角定規の組み合わせにあるヤツです。AB：BH：AH＝2：1：√3です。つまりAHの長さは4.5と言う事になるのです。三角形ABCの面積は1／2×BC×AH＝1／2×12×4.5＝27と言う事がわかります。

今日の教訓　　30°、45°、60°を見たら、三角定規を連想せよです