長方形の面積が40㎠であるとき、下の色の付いた図形の面積を求めなさい。
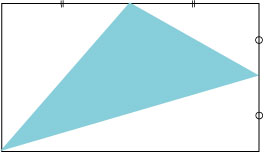
この問題はかなり頭を柔らかくしないと解けません。
方針は、「四角形の面積から残りの3つの三角形の面積を引く」です。
まずは補助線を引きます。下図の赤線の部分です。残りの三角形をそれぞれ
S1、S2、S3としました。
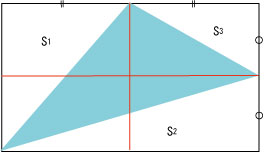
色の付いた三角形があると邪魔なのでまずは取っ払って、S1だけに注目します
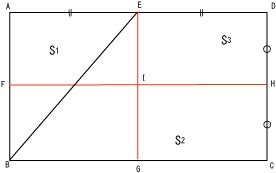
S1の面積は四角形ABGEの半分です。四角形ABGEは、元の四角形の半分ですからS1=10㎠です。
次にS2の面積を考えましょう。
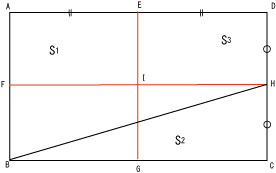
上図を見ると、S2の面積は四角形FBCHの半分です。FBCHは元の四角形の半分ですから、S2=10㎠
では最後にS3の面積を考えましょう。
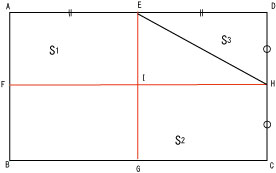
上図を見ると、S3の面積は四角形EIHDの半分です。EIHDは元の四角形の4分の1なので
S3=5㎠です。
これで答を出すことが出来ます。求める面積は40-(S1+S2+S3)=40-(10+10+5)=15㎠です。


